排序算法：堆排序

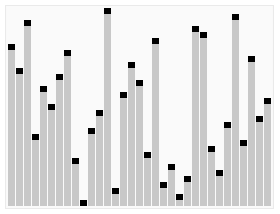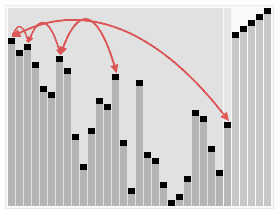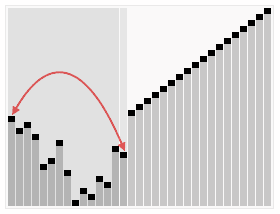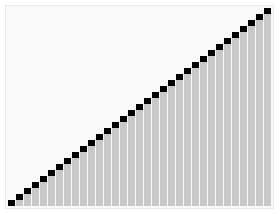
堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点

算法评价

• 平均时间复杂度：O(nlogn)
• 最好情况：O(nlogn)
• 最坏情况：O(nlogn)
• 空间复杂度：O(1)
• 稳定性：不稳定

算法思想

1. 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区。
2. 将堆顶元素 R1 与最后一个元素 Rn 交换，此时得到新的无序区(R1, R2, …, Rn-1)和新的有序区(Rn)，且满足 R[1, 2, …, n-1] <= Rn。
3. 由于交换后新的堆顶 R1 可能违反堆的性质，因此需要对当前无序区(R1, R2, …, Rn-1)调整为新堆，然后再次将 R1 与无序区最后一个元素交换，得到新的无序区(R1, R2 …, Rn-2)和新的有序区(Rn-1, Rn)。不断重复此过程直到有序区的元素个数为 n-1，则整个排序过程完成。

代码示例

Javascript

function heapSort(array) {

    function swap(array, i, j) {
        var temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

    function maxHeapify(array, index, heapSize) {
        var iMax,
            iLeft,
            iRight;
        while (true) {
            iMax = index;
            iLeft = 2 * index + 1;
            iRight = 2 * (index + 1);

            if (iLeft < heapSize && array[index] < array[iLeft]) {
                iMax = iLeft;
            }

            if (iRight < heapSize && array[iMax] < array[iRight]) {
                iMax = iRight;
            }

            if (iMax != index) {
                swap(array, iMax, index);
                index = iMax;
            } else {
                break;
            }
        }
    }

    function buildMaxHeap(array) {
        var i,
            iParent = Math.floor(array.length / 2) - 1;

        for (i = iParent; i >= 0; i--) {
            maxHeapify(array, i, array.length);
        }
    }

    function sort(array) {
        buildMaxHeap(array);

        for (var i = array.length - 1; i > 0; i--) {
            swap(array, 0, i);
            maxHeapify(array, 0, i);
        }
        return array;
    }

    return sort(array);
}