排序算法：计数排序

计数排序是一个非基于比较的排序算法，该算法于 1954 年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为 Ο(n+k)（其中 k 是整数的范围），快于任何比较排序算法

算法评价

• 平均时间复杂度：O(n + k)
• 最好情况：O(n + k)
• 最坏情况：O(n + k)
• 空间复杂度：O(k)
• 稳定性：稳定

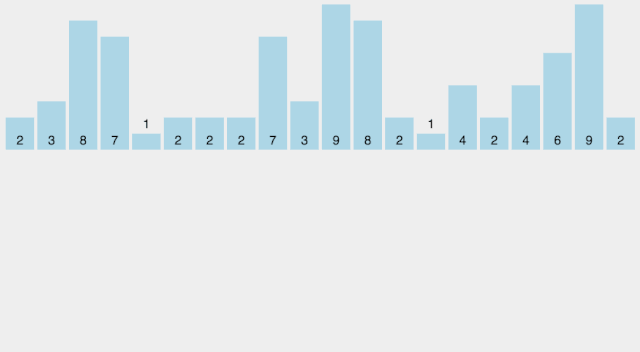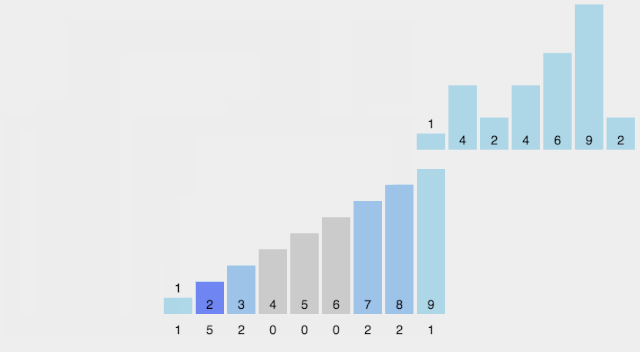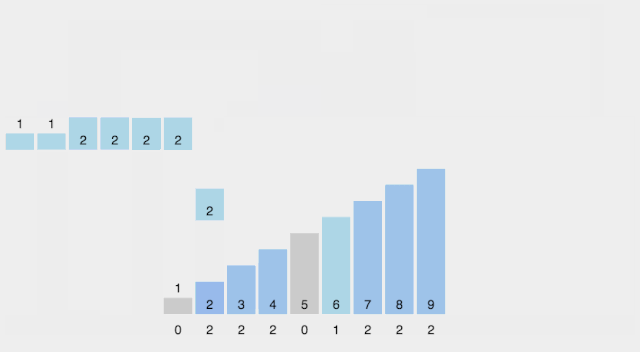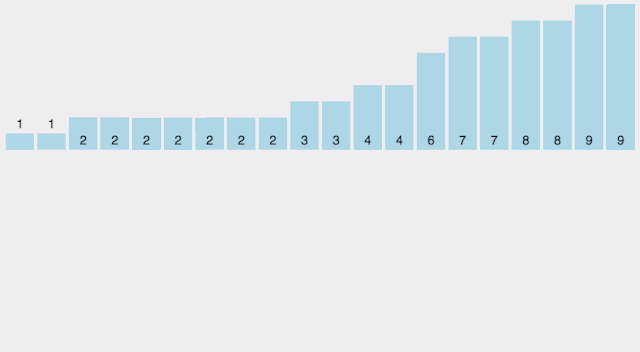
算法思想

1. 找出待排序的数组中最大和最小的元素。
2. 统计数组中每个值为 i 的元素出现的次数，存入数组 C 的第 i 项。
3. 对所有的计数累加（从 C 中的第一个元素开始，每一项和前一项相加）。
4. 向填充目标数组：将每个元素 i 放在新数组的第 C[i] 项，每放一个元素就将 C[i] 减去 1。

代码示例

Javascript

Array.prototype.countSort = function() {
    let len = this.length
    if (len < 2) {
        return
    }
    // 桶数组
    var suportArr = new Array(len + 1);
    // 结果数组
    var resArr = new Array(len);
    // 初始化桶数组
    for (i = 0; i < suportArr.length; i++) {
        suportArr[i] = 0;
    }
    // 待排序数组中的数组出现，在桶子对应位置+1代表这个数出现的个数+1了
    for (let i = 0; i < len; i++) {
        suportArr[arr[i]]++;
    }
    // 从第1项开始，桶数组加上前一个桶的个数，现在辅助数组的意义变成了每一项的排名了。
    for (let i = 1; i < suportArr.length; i++) {
        suportArr[i] += suportArr[i - 1];
    }
    // 根据辅助数组的排名，从后往前赋值
    for (let i = len - 1; i >= 0; i--) {
        resArr[suportArr[arr[i]] - 1] = arr[i];
        suportArr[arr[i]]--;
    }
    // 这里this不能直接赋值数组，我们就只能采取splice剪切数组再替换新的
    this.splice(0, this.length, resArr)
}