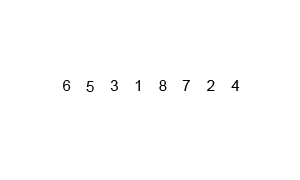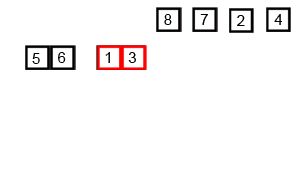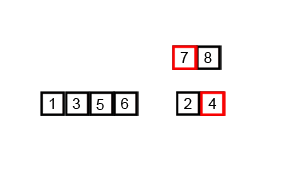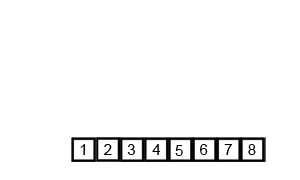归并排序(Merge Sort)是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用
算法评价
- 平均时间复杂度:O(nlogn)
- 最好情况:O(nlogn)
- 最坏情况:O(nlogn)
- 空间复杂度:O(n)
- 稳定性:稳定
算法思想
- 把长度为 n 的输入序列分成两个长度为 n/2 的子序列。
- 对这两个子序列分别采用归并排序。
- 将两个排序好的子序列合并成一个最终的排序序列。
实例分析
以数组 array = [6, 5, 3, 1, 8, 7, 2, 4] 为例,首先将数组分为长度为 2 的子数组,并使每个子数组有序:
[6, 5] [3, 1] [8, 7] [2, 4]
↓ ↓ ↓ ↓
[5, 6] [1, 3] [7, 8] [2, 4]然后再两两合并:
[6, 5, 3, 1] [8, 7, 2, 4]
↓ ↓
[1, 3, 5, 6] [2, 4, 7, 8]最后将两个子数组合并:
[6, 5, 3, 1, 8, 7, 2, 4]
↓
[1, 2, 3, 4, 5, 6, 7, 8]排序过程动画演示如下:
代码示例
Javascript
function mergeSort(array) {
function sort(array, first, last) {
first = (first === undefined) ? 0 : first
last = (last === undefined) ? array.length - 1 : last
if (last - first < 1) {
return;
}
var middle = Math.floor((first + last) / 2);
sort(array, first, middle);
sort(array, middle + 1, last);
var f = first,
m = middle,
i,
temp;
while (f <= m && m + 1 <= last) {
if (array[f] >= array[m + 1]) { // 这里使用了插入排序的思想
temp = array[m + 1];
for (i = m; i >= f; i--) {
array[i + 1] = array[i];
}
array[f] = temp;
m++
} else {
f++
}
}
return array;
}
return sort(array);
}